Dernière modification le 17 novembre 2021
Je le répète assez souvent : « l’Intelligence Artificielle peut nous rendre des services dans le NetDevOps » pour résoudre des problèmes qui nécessiteraient des algorithmes très longs basés sur des successions de tests. Pour illustrer concrètement ces propos, je vous propose d’étudier un cas simple d’application de l’apprentissage automatique.
Prenons un exemple qui pourrait parfaitement faire partie d’un test de QI. Soit la suite de nombre suivante :
| X | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| Y | -3 | -1 | 1 | 3 | 5 | 7 | ? |
Compléter la dernière valeur de Y manquante…
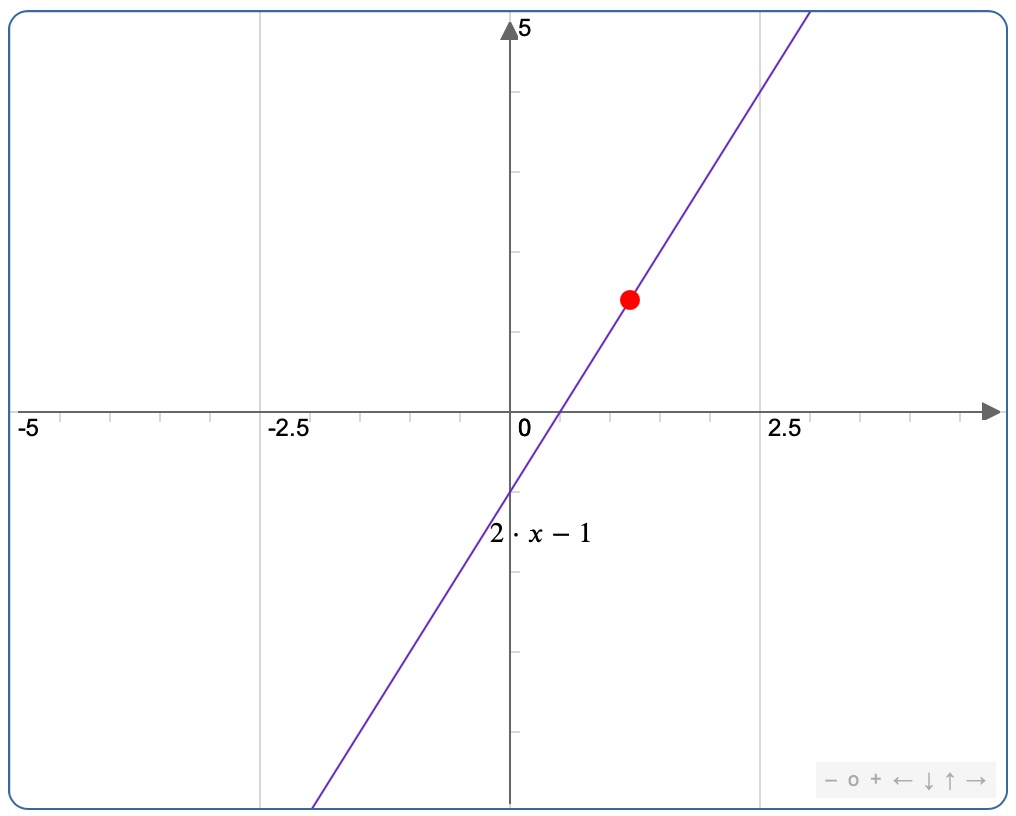
Pour résoudre ce problème, il va falloir trouver la relation qui relie X et Y et une fois trouvée, l’appliquer à la valeur manquante. Un oeil un peu entrainé va rapidement voir que la relation est Y = 2X – 1
Par soucis de validation, on pourra l’appliquer à chacun des X pour vérifier qu’on a trouvé la relation avec certitude. Une fois validée, la relation sera appliquée à la dernière valeur de X pour trouver Y = 9. Cette relation pourrait s’appliquer à de nouvelles valeurs de X.
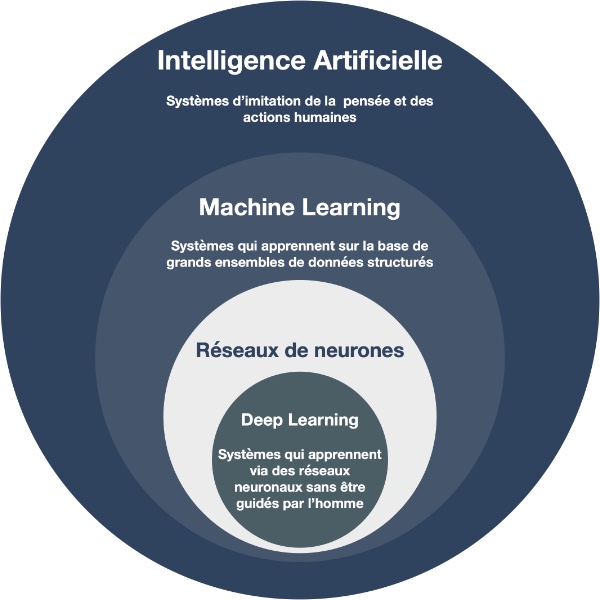
Maintenant, qu’en est-il pour faire traiter ce problème par la machine et lui faire reproduire un raisonnement proche de celui que nous avons utilisé ? Il faut faire appel à un domaine de l’Intelligence Artificielle qui est l’apprentissage automatique (Machine Learning) avec la stratégie de « Supervised Learning ». Avec le langage Python, l’outil TensorFlow représente, de loin, la meilleure approche.
En développement traditionnel, on doit fournir des règles en même temps que les données pour trouver une réponse.
Dans une approche « Machine Learning », on passe par une étape qui consiste à créer un modèle pour l’utiliser ensuite afin de prédire une réponse.
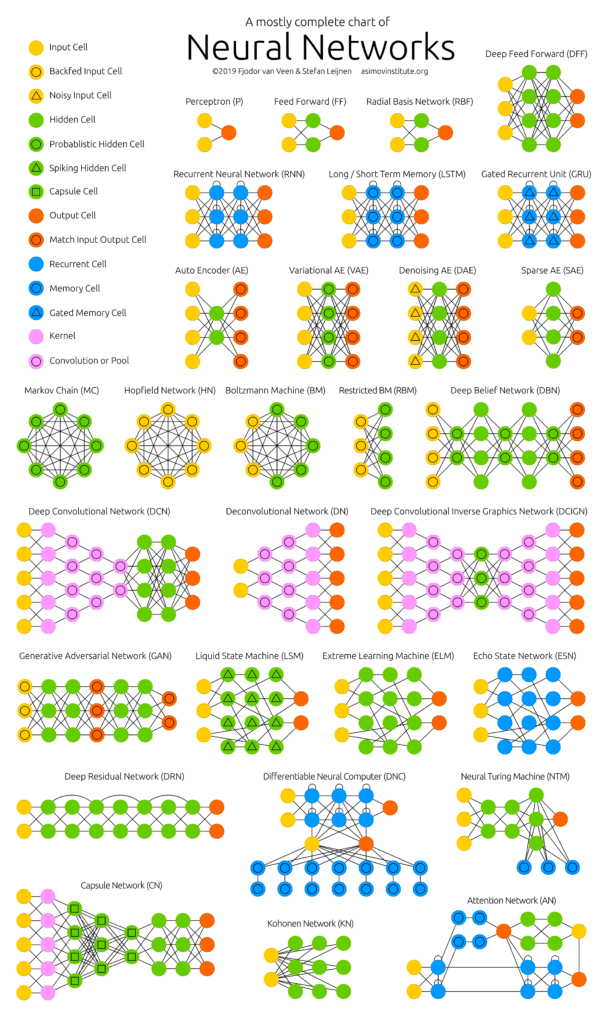
Un réseau est un ensemble de neurones organisés en couches et reliés entre eux par des connexions appelées des poids. Chacun de ces poids est une valeur qui va servir à propager les informations. Ils sont à la base du fonctionnement du réseau et c’est à partir d’eux que tout l’apprentissage pourra se faire. La première couche de neurones d’entrée s’appelle le « Input Layer » et la couche de neurones de sortie s’appelle le « Output Layer ». Les couches qui se trouvent entre « Input » et « Output » s’appellent les « Hidden Layers » et leur nombre peut varier de zéro à l’infini sachant que pour parler de Deep Learning il faut au moins deux « Hidden Layers ».
Chaque neurone prend une valeur numérique dépendante de toutes ses connexions entrantes en fonction de leurs poids associés et qui définit son niveau d’activation. Le degré d’activation de chacun des neurones de la couche « Output » représente le pourcentage de chance que le résultat soit celui-ci. Idéalement, tous les neurones de la couche « Output » devrait rester éteints sauf celui dont le résultat est juste. L’apprentissage va consister à chercher des valeurs de poids qui donneront le meilleur résultat. En comparant le résultat obtenu avec celui qui était attendu on obtient le « Cost » qui, plus il est élevé, plus il indique que le résultat est éloigné de ce qui était attendu.
Le procédé de « Feedforward » correspond au fait de calculer la valeur résultante envoyée à la fonction d’activation. Chaque neurone est composé d’une fonction d’activation (une fonction qui prend un nombre en entrée et renvoie un résultat). On fait une moyenne pondérée des entrées qu’on multiplie par leurs poids correspondants, puis on rajoute un biais qui est une valeur caractéristique à chaque neurone.
Le procédé de « Backpropagation » correspond au fait de corriger les poids qui ont conduit à l’erreur et de s’y prendre couche par couche en utilisant le « Gradient Descent » (recherche de la dérivée nulle correspondant au « Cost » minimum).
La reproduction des étapes de « Feedforward » et de « Backpropagation » conduit à avoir le résultat optimal.
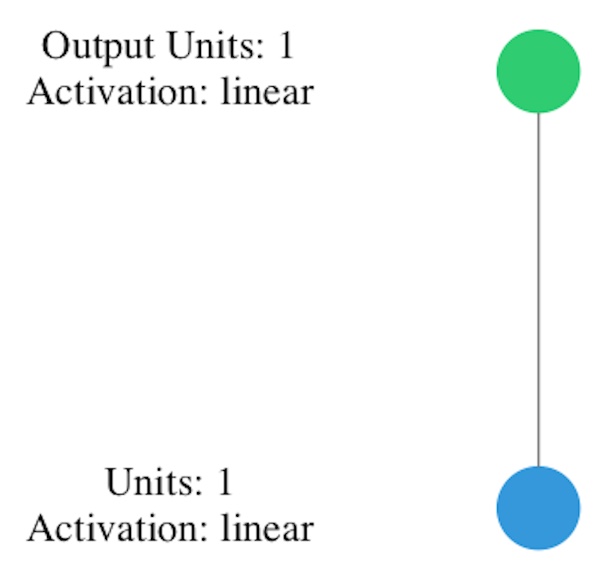
Nous allons créer un modèle appris par la machine, qui va déterminer la relation entre les nombres. Un modèle est un réseau neuronal entrainé. Dans notre cas, une couche unique avec un seul neurone suffira (units=1), tout en introduisant, dans le réseau neuronal, une valeur unique X (input-shape=[1]) et en lui demandant de prédire la valeur de Y.
Pour compiler le modèle, il y a deux fonctions fondamentales pour l’apprentissage automatique : l’erreur et l’optimiseur. Le modèle devine la relation entre les nombres et lors de son entrainement il détermine la médiocrité de la prévision grâce à la fonction d’erreur, puis, l’algorithme utilise la fonction d’optimisation pour générer une autre estimation. L’algorithme du gradient stochastique (Stochastic Gradient Descent – SGD) est une méthode de descente de gradient (itérative) utilisée pour la minimisation d’une fonction objectif qui est écrite comme une somme de fonctions différentiables. En statistiques, l’erreur quadratique moyenne d’un estimateur θ̂ d’un paramètre θ de dimension 1 (Mean Squared Error – MSE) est une mesure caractérisant la « précision » de cet estimateur. Elle est plus souvent appelée « erreur quadratique », mais aussi « risque quadratique ».
La combinaison de ces deux fonctions nous rapproche progressivement de la formule pour obtenir la relation exacte entre les nombres. Dans l’exemple ci-dessous, il répètera cette action 500 fois : faire une prévision, calculer sa précision et calculer l’optimisation pour améliorer cette prévision.
#!/usr/bin/env python import tensorflow as tf from tensorflow import keras import numpy as np import os # Limit log level os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # Define our model model = keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])]) model.compile(optimizer='sgd', loss='mean_squared_error') # Training data X = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float) Y = np.array([-3.0, -1.0, 1.0, 3.0, 5.0, 7.0], dtype=float) # Build model model.fit(X, Y, epochs=500) # Try the model print(model.predict([5.0]))
Les données sont configurées comme un tableau de X et de Y. Le processus de mise en correspondance entre elles est conforme à la méthode d’ajustement du modèle. Une fois terminé, on obtient un modèle entraîné qui peut être utilisé pour prédire des valeurs de Y en fonction de X.
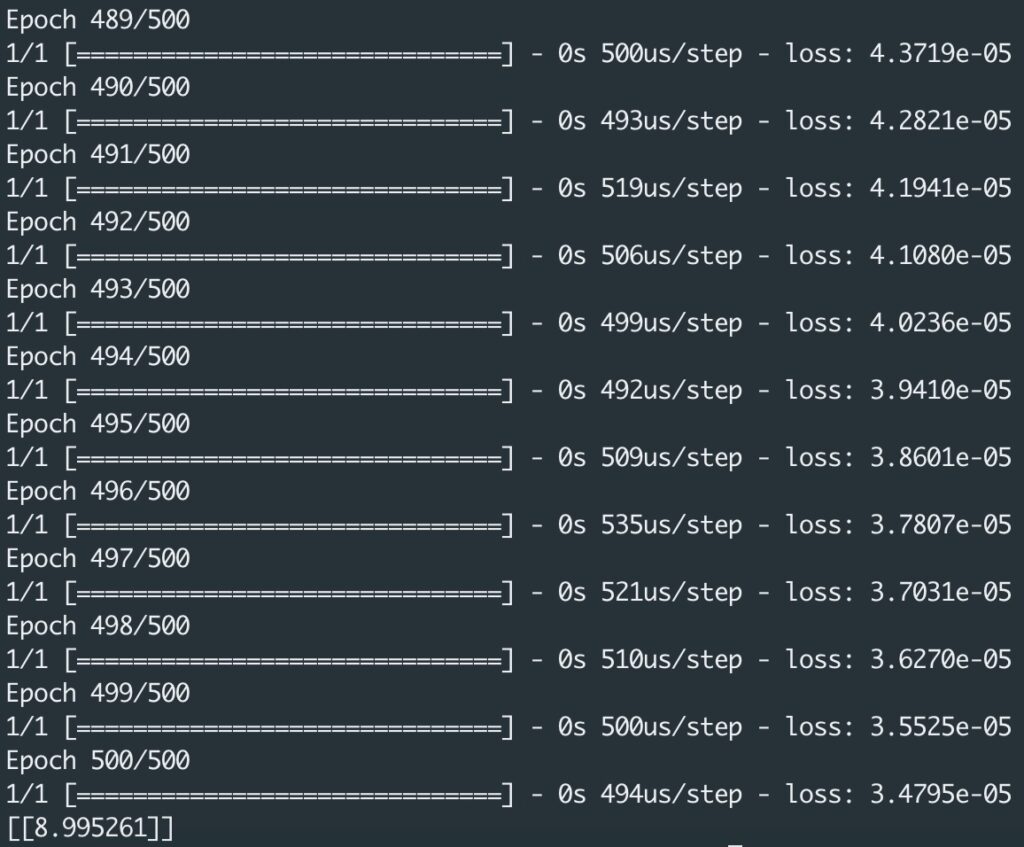
Si vous essayez ce code, vous allez voir la valeur loss diminuer pour représenter une précision de plus en plus fine. Il n’est peut être pas nécessaire d’utiliser 500 epochs, et des essais d’apprentissage peuvent être fait avec d’autres valeurs. Si vous augmentiez beaucoup le nombre d’epochs et si vous utilisiez un réseau de neurones plus complexe pour traiter un autre type de problème, vous noteriez que le temps de traitement s’allongerait beaucoup. Ceci explique que des nouveaux modèles de SBC (Single Board Computer) viennent compléter, dans le domaine de l’Intelligence Artificielle, la panoplie des Raspberry Pi et de ses alternatives.
Vous pensiez trouver la valeur 9 à la fin ? En réalité vous allez obtenir une valeur comme 8.995261, car l’algorithme a été entrainé pour ne faire correspondre que six paires de nombres. Il est fort probable que la fonction soit une ligne droite, mais on ne peut pas en être certain et cette probabilité est intégrée à la prévision. Le résultat annoncé est très proche de la valeur attendue, mais pas la valeur elle même. Travailler avec des réseaux de neurones consiste à traiter presque toujours des probabilités, pas des certitudes…
Une nouvelle approche dans l’algoritmie, qui peut rendre des services dans les développements Python ou JavaScript…